Una nueva conjetura sobre números primos..."Conjetura Fibonapri"

Sea la secuencia Fibonacci 0,1,1,2,3,5,8,13,21,34,55... cuya definición matemática es la siguiente:

Conjetura Fibonapri

Sea fn un elemento de la secuencia de Fibonacii...

Para todo fn >2 e impar y también incluyendo a fn=2 ,la fórmula (fn ^2)-2 entonces genera siempre a un número Primo.

Experimentación...

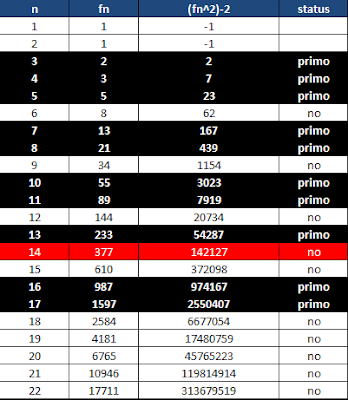
Procedemos someterla a experimentación a través de un software Matemático y obtenemos:

En la tabla observamos que se cumple para n menor a 14.

Pero cuando n=14 tenemos que fn=377 entonces (fn^2)-2 genera a 142127 lo cual no es un número primo ya que es divisible entre el 1,142127 y 311,esto nos es suficiente como contraejemplo para invalidar la conjetura.

Podemos percatar que para el caso n=16 y n=17 (fn^2)-2 genera números primos.

Un vez refutada la conjetura podemos obtener otra conjetura, quien se atreve a probarla?

¿¿¿La fórmula (fn^2)-2 para fn >2 e impar incluyendo a fn=2 sólo genera a los primos 2,7,23,167,439,3023,7919,54287,974167,2550407 ???

Autor:José Camacho Medina