Ecuaciones - Aproximaciones con Números Primos

Les comparto unas Ecuaciones-Aproximaciones que desarrollé recientemente, donde se relaciona a los números primos con constantes importantes en el campo de la matemática, constantes como El Número de Oro, La Constante Copeland – Erdos , Número de Euler.

La primer expresión que tenemos es:

Esta expresión nos afirma que el Número de Oro es igual o casi igual a la suma de la Constante Copeland – Erdos (que resulta de la concatenación de Números Primos después del punto decimal) con el número primo tres y toda esa expresión dividida por el número primo dos.

Tras una experimentación en software Matemático nos podemos dar cuenta que tiene una precisión de tres dígitos.

Otra de las aproximaciones interesantes que descubrí relaciona a la Constante Copeland-Erdos, El Número de Oro y al Número de Euler, la expresión nos dice que:

Tras una experimentación en software Matemático nos podemos dar cuenta que tiene una precisión de dos dígitos.

AUTOR:

M.M.E.A e I.S.C. JOSÉ DE JESÚS CAMACHO MEDINA

FÓRMULA QUE SIEMPRE GENERA NÚMEROS PRIMOS

Les comparto tres nuevas fórmulas que descubrí recientemente las cuales siempre generan a Números Primos, aunque dichos Primos se van repitiendo la fórmula siempre los genera al infinito, la demostración es fácil de concretarse. A continuación les comparto las fórmulas con las imagenes de sus pruebas en un software matemático, la demostración se las dejo de tarea por ser demasiado obvia y sencilla:

Siempre se generan a los Números Primos 2 , 3 y 5 una y otra vez, los primeros 500 valores:

Las otras dos fórmulas:

La fórmula (A) genera siempre a los Primos 2 y 3.

La fórmula (B) genera siempre a el Número Primo 2.

AUTOR: M.M.E.A. e I.S.C. José de Jesús Camacho Medina

FÓRMULA GENERADORA DE NÚMEROS PRIMOS

Una llamarada de los Dioses Matemáticos hicieron que descubriera algunas fórmulas generadoras de números primos las cuales producen resultados sorprendentes en torno a los mismos, les comparto mi descubrimiento en compañía de su análisis. Haremos uso de la Sucesión de Fibonacci: Sea la Sucesión de Fibonacci : 1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , 55 … , la cual se obtiene de :

ANALISIS A TRAVES DE UN SOFTWARE MATEMÁTICO PARA LOS PRIMEROS 1000 VALORES:

Podemos apreciar que para los primeros 1000 valores obtenemos al número ‘1’ ó a Números Primos, los cuales se repiten en algunos casos, si ignoramos a los 1’s y a los duplicados tenemos la siguiente lista de Primos:

5, 13,37, 47, 67, 107, 113,157…

Lo cual nos permite conjeturar que la fórmula genera al número ‘1’ ó a Números Primos en el infinito, con el uso del software demostramos que no siempre produciría estos resultados, se encontrarían contraejemplos que harían no válida la conjetura, de cualquier forma se obtienen patrones importantes en torno a los Números Primos y una relación sorprendente con la secuencia de Fibonacci.

Podemos efectuar más cálculos modificando en alguna forma la fórmula descrita anteriormente y obtenemos resultados igualmente de sorprendentes aunque siempre encontrando contraejemplos en la prolongación de la variable natural ‘n’, esto nos posibilita a seguir tratando con este molde de fórmula a fin de encontrar una que generé siempre a números primos y sea desconocida para el universo matemático.

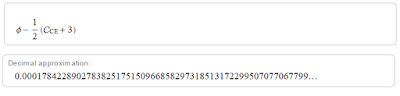
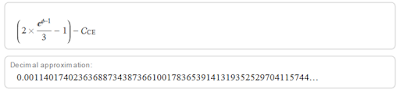
Otras formas alternativas de nuestra fórmula:

AUTOR: M.M.E.A. e I.S.C. José de Jesús Camacho Medina