Primero de adentrarnos a la relación que existe entre el Triángulo de Pascal y Los Números Primos, les comparto un video introductorio acerca del Triángulo de Pascal:

Conjetura PriPascal
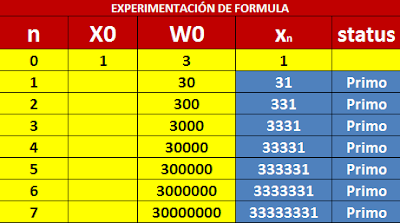
 Los primeros valores arrojados por la conjetura son los siguientes:
Los primeros valores arrojados por la conjetura son los siguientes:
2,3,2,5,1,7,2,3,1,11,1,13,1,1,2,17...
Cómo podemos ver en el triángulo de Pascal se encuentra un universo de propiedades matemáticas extraordinarias, me di a la tarea de investigar si en el triángulo existia relación con los números Primos y encontre lo siguiente:
Si en una fila el primer número después del 1 es un número primo se cumple que todos los demás números de esa fila son divisibles por ese número primo excluyendo a los 1 's. Por ejemplo, en la fila 1-7-21-35-35-21-7-1 el primer número después del 1 es el 7, que es primo,nos podemos percatar que7,21,35,35,21,7 son divisibles por siete, por ende , analizamos una relación entre los coeficientes binomiales que aparecen en el triángulo de pascal.Es entonces que podemos utilizar el triángulo de pascal como test de primalidad,elegimos un número y nos ubicamos en la fila de dicho número , si ese número es divisible por los coeficientes binomiales de esa fila exceptuando a los unos, entonces es un Número Primo.
Si en una fila el primer número después del 1 es un número primo se cumple que todos los demás números de esa fila son divisibles por ese número primo excluyendo a los 1 's. Por ejemplo, en la fila 1-7-21-35-35-21-7-1 el primer número después del 1 es el 7, que es primo,nos podemos percatar que7,21,35,35,21,7 son divisibles por siete, por ende , analizamos una relación entre los coeficientes binomiales que aparecen en el triángulo de pascal.Es entonces que podemos utilizar el triángulo de pascal como test de primalidad,elegimos un número y nos ubicamos en la fila de dicho número , si ese número es divisible por los coeficientes binomiales de esa fila exceptuando a los unos, entonces es un Número Primo.

Fué entonces que el interes se manifesto en mi ser y me di a la tarea de explorar y explotar más alla la relación del triángulo con los números Primos, en base a lo susodicho, pude percatarme de una vinculación de los coeficientes binomiales de cada fila del triángulo con el máximo común divisor de los elementos de dicha fila, lo concrete en una conjetura y tras experimentarla en un software me percate que habia un patron del máximo común divisor de los elementos de fila exceptuando al los unos con los coeficientes binomiales , intuyendo que la demostración de la conjetura que a continuación les comparto , no es tan complicada:
Conjetura PriPascal
Sea mn una fila del triangulo de pascal donde n=0,1,2, y sea i una columna donde i=0,1,2,.. Se Representa al K-esimo elemento de fila por ki.
Para toda fila mn donde n>1
M.C.D.{mn} Produce a un número Primo ó al número uno.
Donde M.C.D. Es el Máximo Común Divisor y
mn={ki} Para i=1,..(n-1).
 Los primeros valores arrojados por la conjetura son los siguientes:
Los primeros valores arrojados por la conjetura son los siguientes:2,3,2,5,1,7,2,3,1,11,1,13,1,1,2,17...